数据结构与算法

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间，空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

数组

数组的基本使用

public class TestArray {
    public static void main(String[] args) {
        // 创建一个数组
        int[] arr1=new int[3];

        // 获取数组的长度
        int length = arr1.length;
        System.out.println("arr1's length: "+length);//arr1's length: 3

        // 访问数组中的元素:数组名[下标] 注意：下标从0开始,最大可以取到长度-1
        int element0 = arr1[0];
        System.out.println("element0: " + element0);//element0: 0
        for (int x : arr1) {
            System.out.println(x);//0  0  0
        }

        // 为数组中的元素赋值
        arr1[0]=99;
        System.out.println("element0: " + arr1[0]);//element0: 99
        arr1[1] = 98;
        arr1[2] = 97;

        // 遍历数组
        for (int i=0;i<length;i++){
            System.out.println("arr1 element" + i + ": " + arr1[i]);
            //arr1 element0: 99    arr1 element1: 98    arr1 element2: 97
        }

        // 创建数组的同时为数组中的元素赋值
        int[] arr2 = new int[] { 90, 80, 70, 60, 50 };

        // 获取数组的长度
        System.out.println("arr2 length: " + arr2.length);//arr2 length: 5
    }
}

数组元素的添加

import java.util.Arrays;

public class TestArray {
    public static void main(String[] args) {
        // 解决数组的长度不可变的问题
        int[] arr = new int[] { 9, 8, 7 };

        // 快速查看数组中的元素
        System.out.println(Arrays.toString(arr));// [9, 8, 7]

        // 要加入数组的目标元素
        int dst = 6; // destination 目的地 缩写

        // 创建一个新的数组，长度是原数组长度+1
        int[] newArr = new int[arr.length + 1];

        // 把原数组中的数据全部复制到新数组中
        for (int i = 0; i < arr.length; i++) {
            newArr[i] = arr[i];
        }

        // 把目标元素放入新数组的最后
        newArr[arr.length] = dst;

        // 新数组替换原数组
        arr = newArr;

        System.out.println(Arrays.toString(arr));// [9, 8, 7, 6]
    }
}

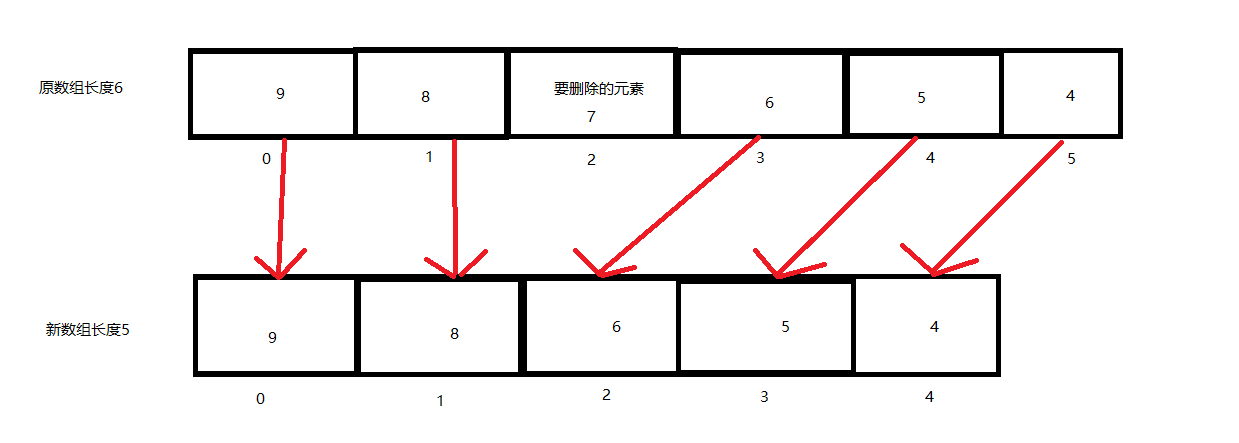
数组元素的删除

import java.util.Arrays;

public class TestArray {
    // 如何删除数组中的元素
    public static void main(String[] args) {
        // 目标数组
        int[] arr = new int[] { 9, 8, 7, 6, 5, 4 }; // 数组长度为6

        System.out.println(arr.length); // 6

        // 要删除的元素的下标
        int dst = 2; //删除7

        System.out.println(Arrays.toString(arr));// [9, 8, 7, 6, 5, 4]

        // 创建一个新的数组，长度是原数组的长度-1
        int[] newArr = new int[arr.length - 1]; // 数组长度为5

        // 复制原数组中除了要删除的那个元素以外其它的元素
        for (int i = 0; i < newArr.length; i++) { // i: 0\1\2\3\4
            // 要删除的元素之前的元素
            if (i < dst) {
                newArr[i] = arr[i];
                // 要删除的元素之后的元素
            } else {
                newArr[i] = arr[i + 1];
            }
        }

        // 新数组替换旧数组
        arr = newArr;

        System.out.println(Arrays.toString(arr));// [9, 8, 6, 5, 4]
    }
}

面向对象的数组

import java.util.Arrays;

public class MyArray {
    // 用于存储数据的数组
    private int[] elements; // 只能存 int, 存其他类型的数据：object

    public MyArray() {
        elements = new int[0];
    }

    // 获取数组长度的方法
    public int size() {
        return elements.length;
    }

    // 往数组的末尾添加一个元素
    public void add(int element) {
        // 创建一个新的数组
        int[] newArr = new int[elements.length + 1];
        // 把原数组中的元素复制到新数组中
        for (int i = 0; i < elements.length; i++) {
            newArr[i] = elements[i];
        }
        // 把添加的元素放入新数组中
        newArr[elements.length] = element;
        // 使用新数组替换旧数组
        elements = newArr;
    }

    // 打印所有元素到控制台
    public void show() {
        System.out.println(Arrays.toString(elements));
    }

    // 删除数组中的元素
    public void delete(int index) {
        // 判断下标是否越界
        if (index < 0 || index > elements.length - 1) {
            throw new RuntimeException("下标越界");
        }
        // 创建一个新的数组，长度为原数组的长度-1
        int[] newArr = new int[elements.length - 1];
        // 复制原有数据到新数组
        for (int i = 0; i < newArr.length; i++) {
            // 想要删除的元素前面的元素
            if (i < index) {
                newArr[i] = elements[i];
                // 想要删除的元素后面的元素
            } else {
                newArr[i] = elements[i + 1];
            }
        }
        // 新数组替换旧数组
        elements = newArr;
    }

    // 取出指定位置的元素
    public int get(int index) {
        // 判断下标是否越界
        if (index < 0 || index > elements.length - 1) {
            throw new RuntimeException("下标越界");
        }
        return elements[index];
    }

    // 插入一个元素到指定位置
    public void insert(int index, int element) {
        // 创建一个新的数组
        int[] newArr = new int[elements.length + 1];
        // 将原数组中的元素放入新数组中。
        for (int i = 0; i < elements.length; i++) {
            // 目标位置之前的元素
            if (i < index) {
                newArr[i] = elements[i];
                // 目标位置之后的元素
            } else {
                newArr[i + 1] = elements[i];
            }
        }
        // 插入新的元素
        newArr[index] = element;
        // 新数组替换旧数组
        elements = newArr;
    }

    // 替换指定位置的元素
    public void set(int index, int element) {
        // 判断下标是否越界
        if (index < 0 || index > elements.length - 1) {
            throw new RuntimeException("下标越界");
        }
        elements[index] = element;
    }

    // 线性查找
    public int search(int target) {
        // 遍历数组
        for (int i = 0; i < elements.length; i++) {
            if (elements[i] == target) {
                return i;
            }
        }
        // 没有找到对应的元素
        return -1;
    }

    // 二分法查找
    public int binarySearch(int target) {
        // 记录开始位置
        int begin = 0;
        // 记录结束位置
        int end = elements.length - 1;
        // 记录中间的位置
        int mid = (begin + end) / 2;
        // 循环查找
        while (true) {
            // 什么情况下没有这个元素？
            // 开始在结束位置之后或重合,没有这个元素
            if (begin >= end) {
                return -1;
            }
            // 判断中间的这个元素是不是要查找的元素
            if (elements[mid] == target) {
                return mid;
                // 中间这个元素不是要查的元素
            } else {
                // 判断中间这个元素是不是比目标元素大
                if (elements[mid] > target) {
                    // 把结束位置调整到中间位置前一个位置
                    end = mid - 1;
                    // 中间这个元素比目标元素小
                } else {
                    // 把开始位置调整到中间位置的后一个位置
                    begin = mid + 1;
                }
                // 取出新的中间位置
                mid = (begin + end) / 2;
            }
        }
    }
}

public class TestArray {
    public static void main(String[] args) {
        // 创建一个可变的数组
        MyArray ma = new MyArray();
        // 获取长度
        int size = ma.size();
        ma.show();// []
        // 往可变数组中添加一个元素
        ma.add(99);
        ma.add(98);
        ma.add(97);
        // 显示可变数组中的所有元素到控制台
        ma.show();// [99, 98, 97]
        // 删除某个元素
        ma.delete(1);
        ma.show();// [99, 97]
        // 取出指定位置的元素
        int element = ma.get(1);
        System.out.println(element); // 97
        ma.add(96);
        ma.add(95);
        ma.add(94);
        ma.show();//[99, 97, 96, 95, 94]
        // 插入元素到指定位置
        ma.insert(3, 93);
        ma.show();// [99, 97, 96, 93, 95, 94]
        // 替换指定位置的元素
        ma.set(0, 100);//[100, 97, 96, 93, 95, 94]
        ma.show();
        System.out.println(ma.size());//6
    }
}

查找算法之线性查找

public class TestArray {

    public static void main(String[] args) {
        // 目标数组
        int[] arr = new int[]{2, 3, 5, 6, 8, 4, 9, 0};
        // 目标元素
        int target = 8;
        // 目标元素所在的下标
        int index = -1;
        // 遍历数组
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == target) {
                index = i;
                break;
            }
        }
        // 打印目标元素的下标
        System.out.println("index:" + index);//index:4
    }
}

查找算法之二分法查找

二分法查找（又叫分半查找、拆半查找）

前提条件：数组必须是一个有序的序列 可以是递增的 也可以是递减的

思想：要查找的数据x，每次与中间的位置的元素进行比较大小，来判断被查找的数据x，可能在 中间的左边 还是 右边